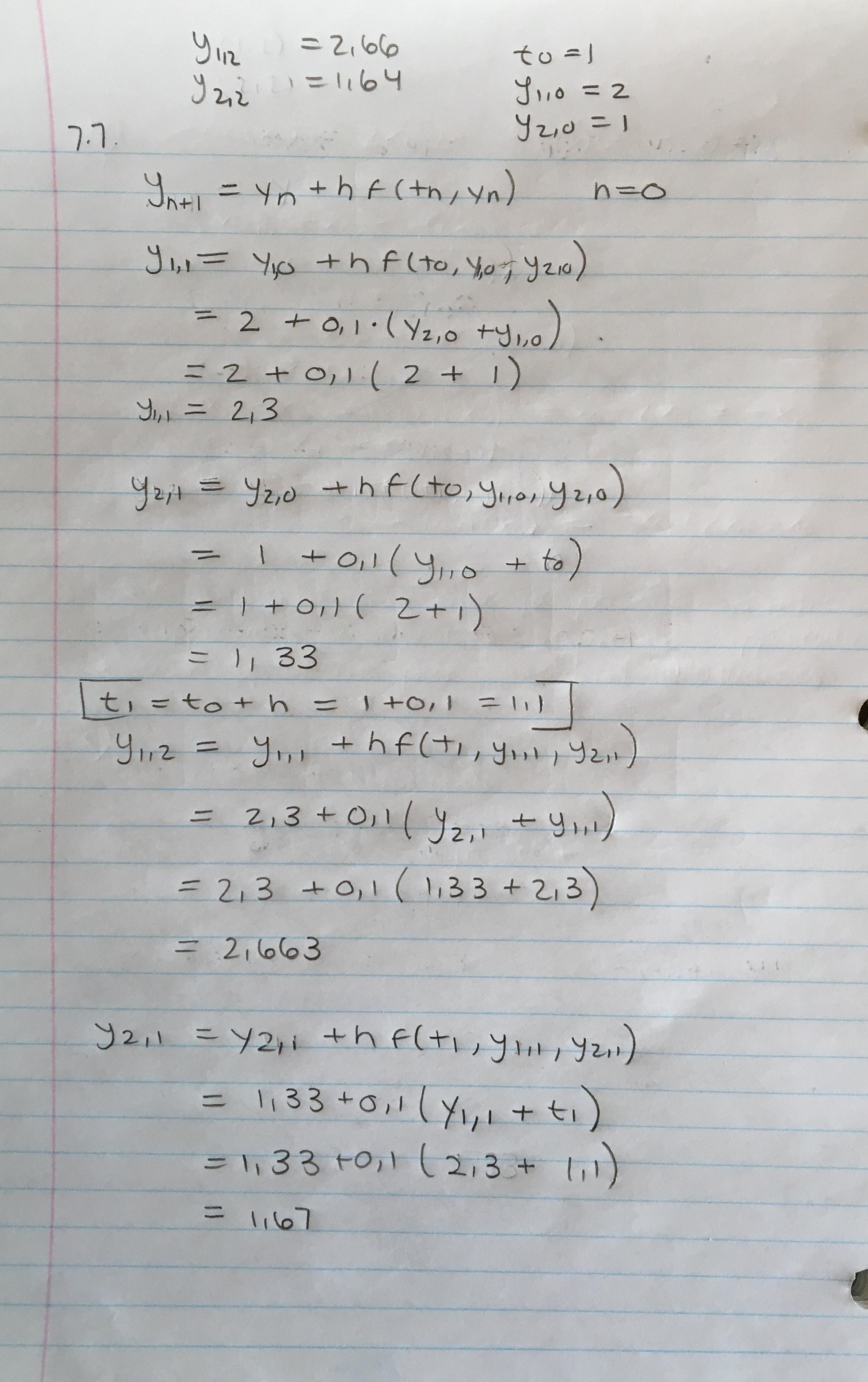Bonjour,
Selon le plan de cours modifié, la méthode de Runge-Kutta a été enlevée. Cependant, le numéro 7.7 du manuel sur les systèmes d'équations du premier ordre nous demande de l'utiliser. Je me demandais donc si nous devions l'étudier ou non.
Merci