Pour le 3e numéro, le vecteur u=u0*[ f(x,y), g(x,y), 0 ] est-ce que chaque terme est une composante de vitesse en x y et z respectivement ? Si c'est le cas le ux représente du/dx ou la composante en x de la vitesse?
Bonjour, la notation est peut-être un peu inconnue pour vous.
le vecteur est u = [ u_x , u_y, u_z] avec (_ xsignifie indice x)
Donc les trois composantes du vecteur u sont ux, uy, uz. Il n'y a pas de dérivées de la vitesse. La vitesse est supposée connue, stable et constante.
C'est bien de vous assurer de cela avant de commencer!
BB
Est-ce que c'est normal que la composante en x soit identique à la composant en y? Je demande parce que le champs vectoriel que j'obtiens à pas vraiment l'air d'un vortex.
Bonjour,
Il y a une erreur dans la composante y de la vitesse ( le sin et le cos sont inversé, ainsi que le signe)
Jcorrigerai cela demain matin et j'enverrai un nouveau message a ce moment.
Merci,
BB
J'aimerais juste vérifier que ce que j'ai fait est correct. Est-ce qu'au centre du bassin à (0,0) on retrouve un température autour de 120'C.
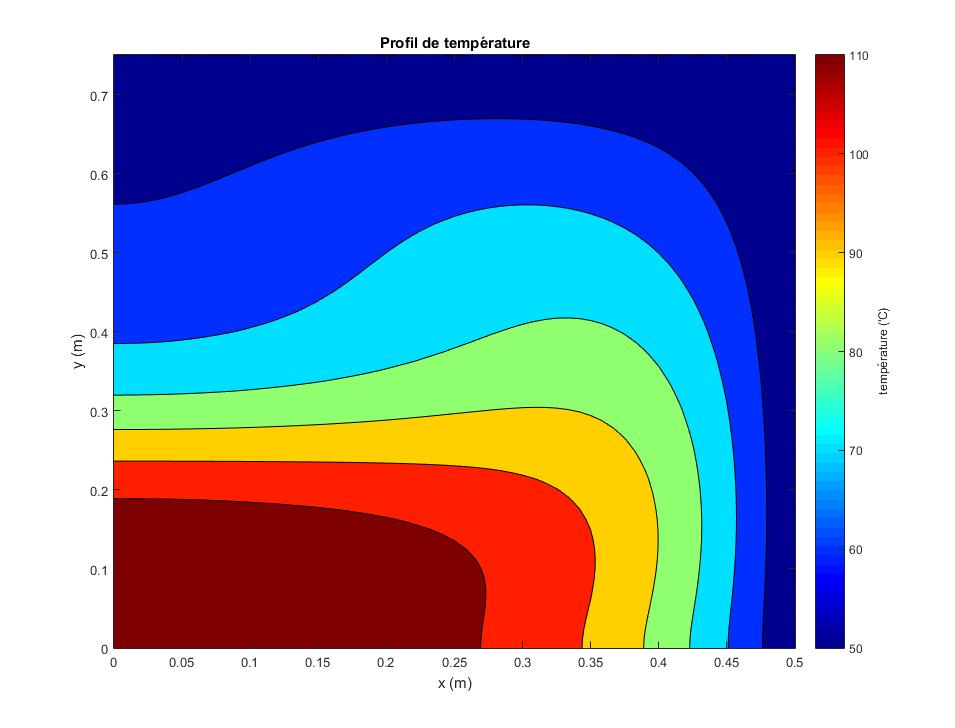
Bonjour,
Je ne peux pas vraiment vérifier vos réponses ainsi.
Néanmoins, regardez si votre profil fait du sens pour S0=0
ensuite pour U=0 regardez le profil que vous obtenez. N'oubliez pas que nous avons une équation de nature elliptique. Ensuite, et seulement ensuite, mettez u0 à la bonne valeur. Essayez par exemple de mettre u0 à la bonne valeur en mettant S0=0, et vérifiez ensuite.
En procédant étape par étape ainsi, vous devriez vous assurer que tout est ok!
Merci
Bruno
PS: beau graphique, j'apprécie.
Du moins, juste être sur d'avoir bien saisit la situation physique du problème. On a un bassin où on a une source de chaleur au centre et on regarde comment les tourbillons affectent le profil de température du bassin. Si u0 est nul cela signifie que le bassin est "calme" et donc que l'on devrait avoir une forte température au centre qui diminue de façon uniforme plus on s'éloigne du centre ?
Exactement.
La forme de la diminution du profil de température dépend de la longueur et de la hauteur de la plaque. Si L = H, alors le profil devrait évidemment prendre la forme d'un cercle, sinon, cela prendra une forme "elliptique".
J'ai découpé mon domaine en 4 et j'ai seuleument regardé le quadrant en haut à droite en mettant des conditions frontières de symétrie (flux nul) sur les côtés gauche et celui d'en bas (dT/dx=0 et dT/dy=0 respectivement). J'ai par la suite dupliqué le résultat obtenu pour avoir une map complet du bassin. Par curiosité j'ai également fait une analyse sur lle bassin au complet sans découpage avec les conditions de 50'C sur chaque côté. Est-ce que c'est normal que les 2 profil que j'obtient soit différent? dans ma tête il devrait être quasi identique.
Nvm je viens de trouver pourquoi mes 2 figurent différentes. (en raison de l'indexation de matlab)